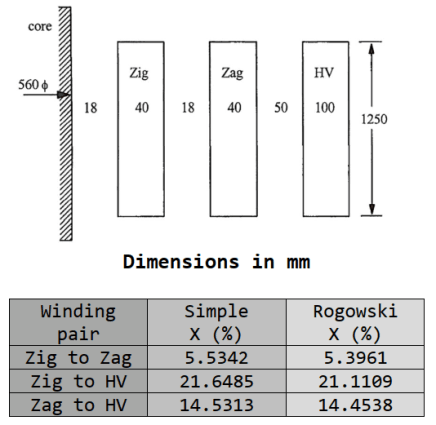
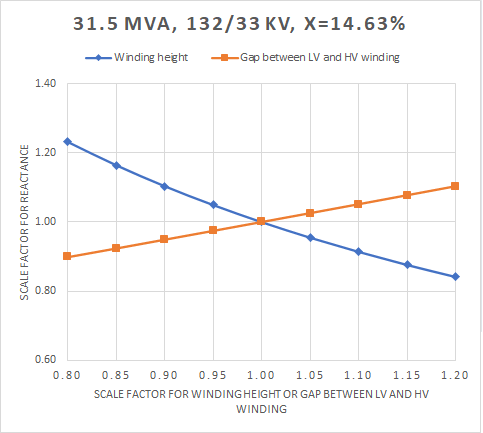
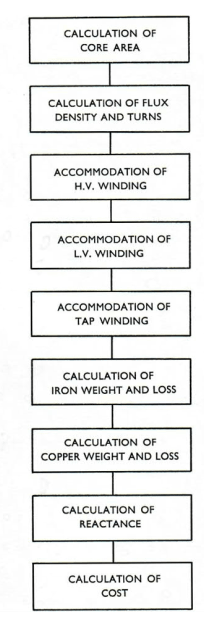
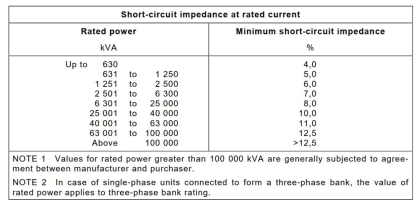
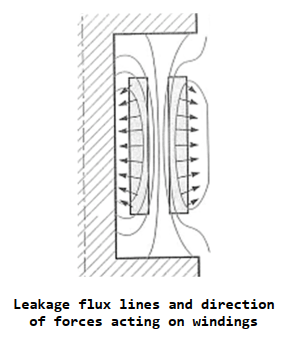
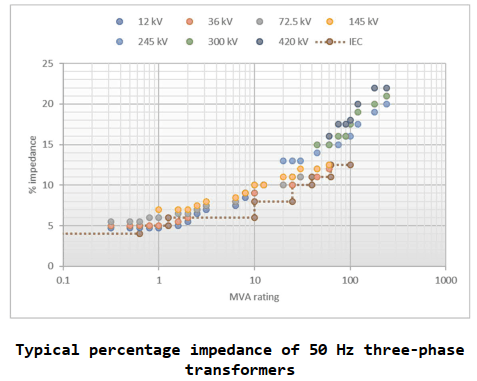
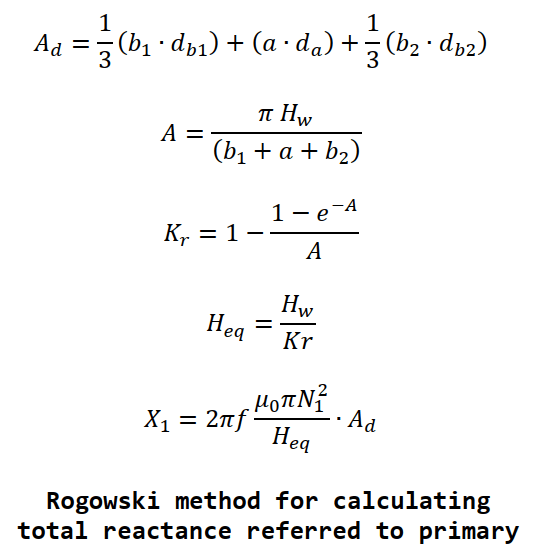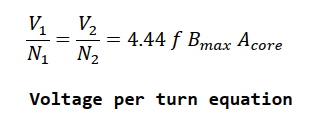Further information
W. Rogowski, “Über das Streufeld und den Streuinduktionskoeffizienten eines Transformators mit Scheiben-Wicklung und geteilten Endspulen,” Verein Deutscher Ingenieure, Mitteilungen über Forschungsarbeiten, Heft 71, Berlin, 1909.
L. F. Blume et al, Transformer Engineering - A treatise on the Theory, Operation and Application of Transformers, John Wiley, Chapman and Hall, 1938.
S Austen Stignat, H Morgan Lacey, J & P Transformer Book, 8th ed, Johnson & Phillips, 1941.
D. McDonald, Power Transformers for high-voltage transmission with special reference to their design, Bruce Peebles and Co. Ltd., 1957.
M. G. Say, Electrical Engineering Design Manual, 3rd ed, Chapman and Hall, 1964.
M. Waters, The Short-Circuit Strength of Power Transformers, McDonald & Co. Ltd, London, 1966.
M.G. Say, Alternating Current Machines, 4th ed, Pitman, 1976.
R. Feinberg, Modern Power Transformer Practice, Wiley, 1979.
K. Karsai et al, Large Power Transformers, Elsevier, 1987.
M. Heathcote, J & P Transformer Book, 12th ed, Newnes, 1998.
IEC 60076-5, Power transformers – Part 5: Ability to withstand short circuit, 2000
S.V.Kulkarni, S.A.Khapardem, Transformer Engineering Design and Practice, Marcel Dekker, 2004.
G. Bertagnolli, Short-circuit duty of power transformers, ABB, 2006.